
Título: NP-completude e condicionamento
Palestrante: Gregorio Malajovich - UFRJ
Data: 22/03/2024 de 10:00h às 12:00h
Horário: 15:10 h
Participação Híbrida
Local: Participação Presencial - Sala C - 118
Link da videochamada: https://youtube.com/live/zymw4NaVY3Y
Link do Canal: https://www.youtube.com/

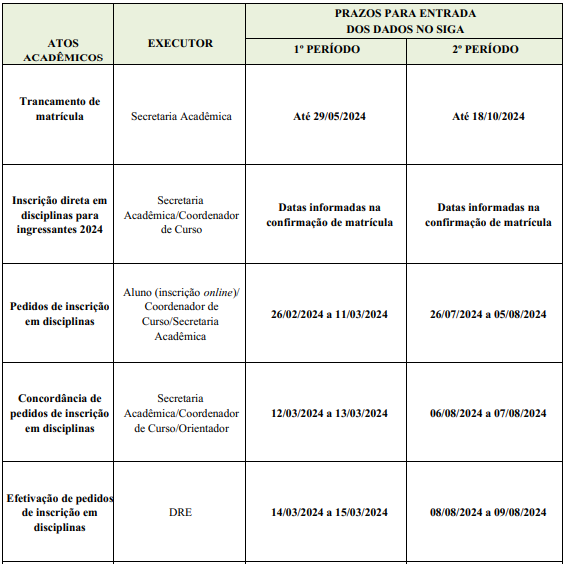
Entre os dias 26 de fevereiro e 11 de março de 2024, estará aberto o período destinado à inscrição em disciplinas na Universidade Federal do Rio de Janeiro (UFRJ).
Solicita-se a atenção dos interessados para que não posterguem este compromisso até o momento derradeiro.
Para mais infomações, clique aqui.
INFORMAÇÕES PRINCIPAIS

Título: Dinâmica de Germes de Difeomorfismos Analíticos Complexos em uma Variável
Palestrante: Renzo Anthony Pino Espinoza
Data: 28/02/2024 de 10:00h às 12:00h
Horário: 10:00h às 12:00h
Fuso Horário: América/São Palulo
Local: Transmissão online
Link da videochamada: https://meet.
